思无邪

个人博客 | 学习，思考，分享

0%

关于Kalman滤波的理解

发表于 更新于 分类于

卡尔曼滤波（Kalman filter）以它的发明者Rudolf. Emil. Kalman先生命名，是一种高效率的递归滤波器（自回归滤波器），它能够从一系列的不完全及包含噪声的测量中，估计动态系统的状态。在控制领域，Kalman滤波被称为线性二次型估计，其也可以认为是一个最优化自回归数据处理算法（optimal recursive data processing algorithm），广泛应用于飞机及太空船的导引、导航及控制。

前言

写在本文之前，有两个重要的思想需贯穿脑海之中：  

    1. 没有绝对准确，只有更为接近的准确
    2. 滤波即为加权  关于1，这个不做多说。

关于2，对信号的滤波即是对离散序列的加权，传统的低通滤波器可以理解为高频权值为0（或接近0），而低频的权值为1，此时便可实现通低频阻高频的效果。同理，高通、带通滤波器可以理解为对不同频段的信号进行加权后获得想要的信号。 

基本概念

 协方差矩阵

设X、Y为随机变量，\(\mu\)、\(\nu\)分别为X、Y的期望。x、y分别为X、Y的真实值，\(\hat{x}\)、\(\hat{y}\)分别为x、y的估计值，则有：

  • 误差：真实值与估计值的差，即\(e=x-\hat{x}\)

  • 方差：方差是描述随机变量与其期望值的离散程度，即\(\sigma_{X}^{2}=E(X-E(X))\)

  • 协方差：描述两个变量间的相关性，\(cov(X,Y)=E[(X-\mu)(Y-\nu)]\) 。其中，X与Y的不相关是独立的必要不充分条件，但是对于X、Y正态分布时二者独立是不相关的充要条件。

  • 协方差矩阵：若\(\mathrm{X}\)为m维向量\(\mathrm{X}=(X_{1},X_{2},…,X_{m})\)，其中\(X_{k}\)中含一组数据；\(\mathrm{Y}\)为n维向量\(\mathrm{Y}=(Y_{1},Y_{2},…,Y_{n})\)，其中\(Y_{k}\)中含一组数据,则\(\mathrm{X}\)与\(\mathrm{Y}\)的协方差应表示为mxn维协方差矩阵： \[ cov(\mathrm{X},\mathrm{Y})=E((\mathrm{X}-\mathrm{\mu})(\mathrm{Y}-\mathrm{\nu})^{T})= \begin{bmatrix} E[(X_{1}-\mu_{1})(Y_{1}-\nu_{1})] & E[(X_{1}-\mu_{1})(Y_{2}-\nu_{2})] &\cdots &E[(X_{1}-\mu_{1})(Y_{n}-\nu_{n})] \\  E[(X_{2}-\mu_{2})(Y_{1}-\nu_{1})]& E[(X_{2}-\mu_{2})(Y_{2}-\nu_{2})] & \cdots  &E[(X_{2}-\mu_{2})(Y_{n}-\nu_{n})] \\  \vdots                                         & \vdots    & \ddots    & \vdots\\ E[(X_{m}-\mu_{m})(Y_{1}-\nu_{1})]&  E[(X_{m}-\mu_{m})(Y_{2}-\nu_{2})]& \cdots  & E[(X_{m}-\mu_{m})(Y_{n}-\nu_{n})] \end{bmatrix} \] 对于\(\mathrm{X}\)自身而言，其协方差矩阵(或称为方差，详见协方差矩阵)： \[ cov(\mathrm{X},\mathrm{X})=E((\mathrm{X}-\mathrm{\mu})(\mathrm{X}-\mathrm{\mu})^{T})= \begin{bmatrix} E[(X_{1}-\mu_{1})(X_{1}-\mu_{1})] & E[(X_{1}-\mu_{1})(X_{2}-\mu_{2})] &\cdots &E[(X_{1}-\mu_{1})(X_{n}-\mu_{n})] \\  E[(X_{2}-\mu_{2})(X_{1}-\mu_{1})]& E[(X_{2}-\mu_{2})(X_{2}-\mu_{2})] & \cdots  &E[(X_{2}-\mu_{2})(X_{n}-\mu_{n})] \\  \vdots                                         & \vdots    & \ddots    & \vdots\\ E[(X_{m}-\mu_{m})(X_{1}-\mu_{1})]&  E[(X_{m}-\mu_{m})(X_{2}-\mu_{2})]& \cdots  & E[(X_{m}-\mu_{m})(X_{n}-\mu_{n})] \end{bmatrix} \] 可以从上式可以看出，矩阵对角为\(\mathrm{X}\)列向量的方差。若\(\mathrm{X}\)服从正态分布，其为对角矩阵。（后面可将\(\mathrm{X}\)联想为状态向量，\(X_{1}\)、\(X_{2}\)联想为位移向量和速度向量）

  • 误差的协方差矩阵：若\(\mathrm{X}\)为m维向量\(\mathrm{X}=(X_{1},X_{2},…,X_{m})\)，其中\(X_{k}\)中含一组数据，误差为m维向量\(\mathrm{e}\)，则其误差的协方差矩阵为： \[ P=cov(\mathrm{e},\mathrm{e})=E[\mathrm{e} \mathrm{e}^{T}] \] 可知，其对角元素元素之和（或称迹）即为均方差。

 注：此处十分重要，将状态变量的误差协方差矩阵与状态变量的最小均方差估计联系起来。

最小均方误差估计

  • 均方误差：它是"误差"的平方的，也就是多个样本的时候，均方差等于每个样本的误差平方再乘以该样本出现的概率的和，即 \[ MSE=E[(x-\hat{x})^{2}]=E[e^{2}] \] 若\(\mathrm{X}\)为m维向量\(\mathrm{X}=(X_{1},X_{2},…,X_{m})\)，其中\(X_{k}\)中含一组数据，则\(\mathrm{X}\)的均方误差：

\[ MSE=E[(\mathrm{x}-\mathrm{\hat{x}})^{T}(\mathrm{x}-\mathrm{\hat{x})}]=E[\mathrm{e}^{T}\mathrm{e}]=tr(E[\mathrm{e}\mathrm{e}^{T}])=\sum_{i=1}^{m}E[\mathrm{e}_{i}^{2}] \]

​ 注意，这里的\(\mathrm{e}\)为m维向量，\(\mathrm{X}\)的均方误差即为误差平方和的期望值，或误差平方的期望之和，这即是误差协方差矩阵的迹。

  • 最小均方差（MMSE）：对于变量\(\mathrm{X}\)，求其某一估计值，使均方误差最小，其最小均方误差即为：

\[ MMSE=MSE_{min}=E[(\mathrm{x}-\mathrm{\hat{x}})^{T}(\mathrm{x}-\mathrm{\hat{x})}]=E[\mathrm{e}^{T}\mathrm{e}]=tr(E[\mathrm{e}\mathrm{e}^{T}])=\sum_{i=1}^{m}E[\mathrm{e}_{i}^{2}] \]

  • 最小均方误差估计：最小均方误差估计即最优估计，即寻找合适的估计函数\(\hat{x}=c(x)\)来估计x，使上式最小。 （1）\(\mathrm{X}\)为一维变量时，该估计函数为： \[ \hat{x}=E[X] \] 其证明详见参考文献，大致过程是通过\(MSE_{min}\)对\(\hat{x}\)求导，令导函数为0，即可求得\(\hat{x}\) 。  
    （2）当\(\mathrm{X}\)存在先验条件\(\mathrm{Y}\)时，该估计函数为： \[ \hat{x}=E[X|Y=y] \] 此时，该估计函数即为\(\mathrm{X}\)在\(\mathrm{Y}\)条件下的条件期望。其证明详见参考文献，证明过程同上。 （3） 当\(\mathrm{X}\)存在先验条件\(\mathrm{Y}\)，且\(\mathrm{X}\)、\(\mathrm{Y}\)为m维向量时，该估计函数为：

\[ \hat{x}(x_{1},x_{1},···,x_{m})=E[X|Y_{1}=y_{1},Y_{2}=y_{2},···,Y_{m}=y_{m}] \]

状态描述

机器人的状态，是指一组完整描述它随时间运动的物理量，比如位置、角度和速度，状态估计即是在包含噪声的测量值中估计机器人的状态值，均方误差越小，估计值越接近真实值。

根据牛顿运动规律，物体的运动方程大体归结为化成如下形式： \[ m\frac{\mathrm{d}^{2} x}{\mathrm{d} t^{2}}+2\beta \frac{\mathrm{d} x}{\mathrm{d} t}+kx=u(t) \] 化成以下形式：
\[ \ddot{x}-a_{1}\dot{x}-a_{0}x=u(t) \] 再写成方程组形式：
\[ \left\{\begin{matrix}\dot{x}=0\cdot x+1\cdot\dot{x}+0\cdot u(t) & & \\ \ddot{x}=a_{0}x+a_{1}\dot{x}+1\cdot u(t)& & \end{matrix}\right. \] 其矩阵形式： \[ \begin{pmatrix}\dot{x}\\ \ddot{x}\end{pmatrix}=  \begin{pmatrix}0 & 1\\ a_{0}& a_{1}\end{pmatrix}\begin{pmatrix}\ x\\ \dot{x}\end{pmatrix}  +  \begin{pmatrix}\ 0\\ \ 1\end{pmatrix}u(t) \] 化简为： \[ \mathbf{\dot{x}}=\mathbf{Ax}+\mathbf{Bu} \] 如果在方程中加入过程噪声，则有： \[ \ddot{x}=a_{1}\dot{x}+a_{0}x+u(t)+w(t) \] 得到类似矩阵：
\[ \begin{pmatrix}\dot{x}\\ \ddot{x}\end{pmatrix}=  \begin{pmatrix}0 & 1\\ a_{0}& a_{1}\end{pmatrix}\begin{pmatrix}\ x\\ \dot{x}\end{pmatrix}  +\begin{pmatrix}\ 0\\ \ 1\end{pmatrix}u(t)  +\begin{pmatrix}\ 0\\ \ 1\end{pmatrix}w(t) \] 运动方程简化为：
\[ \mathbf{\dot{x}}=\mathbf{Ax}+\mathbf{Bu}+\mathbf{w} \] 其中，A：传输矩阵； x：状态矢量； B：控制矩阵； u：控制矢量； w：过程噪声  

在这里，状态向量\(\mathbf=（x,\dot{x}）\)包含位移和速度的信息。推广到多维空间，状态向量为\(\mathbf=（x_{1},x_{2},...,x_{n};\dot{x_{1}},\dot{x_{2}},...,\dot{x_{n}}）\)，这种方法称为状态空间描述法。

由此得到系统模型框图：

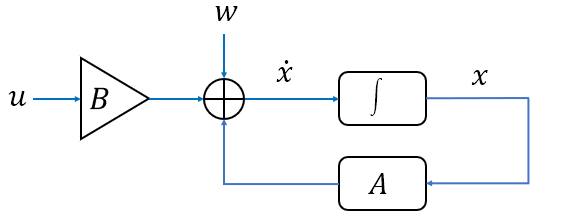
除了物体运动方程，当在x状态处观测，可以得到一个观测方程： \[ \mathbf{z}=\mathbf{Hx}+\mathbf{v} \] 其中，z：观测矢量； H：观测矩阵；v：观测噪声 。

更新以上系统框图，则有：

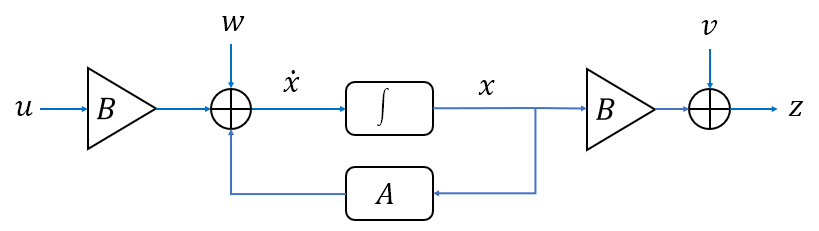
Kalman滤波器

 前提条件

  • 线性系统  
  • 系统噪声和测量噪声服从高斯分布  

 系统模型

卡尔曼滤波建立在线性代数和隐马尔可夫模型上，k时刻的状态在(k-1)时刻的基础上递推过来，系统模型由预测空间模型和观测空间模型组成。在上述运动方程和观测方程基础上，进行离散化并得到状态方程的形式，如下预测空间模型和观测空间模型。

预测空间模型： \[ \mathbf{x_{k}}=\mathbf{Ax_{k-1}}+\mathbf{Bu_{k-1}}+\mathbf{w_{k-1}} \] 其中：

  • \(\mathbf{x_{k}}\)是k时刻的预测状态向量，\(\mathbf{x_{k-1}}\)是(k-1)时刻的状态向量  
  • \(\mathbf{u_{k-1}}\)是(k-1)时刻的控制输入向量
  • \(\mathbf{A}\)是k时刻状态传输矩阵，与系统本身特性相关，其隐含指示(k-1)时刻的状态会影响到k时刻的状态  
  • \(\mathbf{B}\)是k时刻控制输入矩阵，其隐含指示(k-1)时刻的驱动输入会影响到k时刻的状态  
  • \(\mathbf{w_{k}}\)是过程噪声，服从正态分布，\(\mathbf{w_{k}}\sim N(0,Q_{k})\)，\(\mathbf{Q_{k}}\)为其协方差矩阵  

观测空间模型：
\[  \mathbf{z_{k}}=\mathbf{Hx_{k}}+\mathbf{v_{k}}  \] 其中：

  • \(\mathbf{z_{k}}\)是k时刻的观测状态向量  
  • \(\mathbf{H}\)是k时刻的观测矩阵，把真实状态空间映射成观测空间  
  • \(\mathbf{v_{k}}\)是观测噪声，服从正态分布，\(\mathbf{v_{k}}\sim N(0,R_{k})\)，\(\mathbf{R_{k}}\)为其协方差矩阵  

分析上述两个状态方程，不拿看出，在k时刻的预测状态向量\(\mathbf{x_{k}}\)（或观测状态向量\(\mathbf{z_{k}}\)）是在第(k-1)时刻的状态上推导而来（马尔科夫模型），并且都在状态更新的过程中带入新的高斯噪声。离散框图如下：

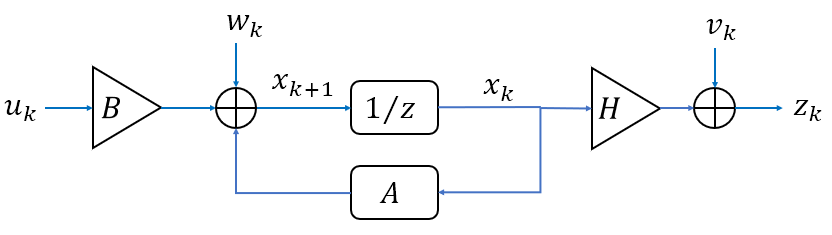
那么问题来了，既然既可以通过预测，亦可以通过观测，来获知系统在k时刻的状态，但是二者都存在误差（噪声），那么二者哪个更可靠呢？这时，我们自然而然的想到了的加权的思想，通过对二者的加权获得k时刻的准确的状态。  通过以下图片可以帮我们更好地理解，小车距出发地的距离可以通过预测模型和测量模型获得，且二者都服从正态分布，都存在误差。通过对二者加权，得到我们想要的较为准确的状态模型（图中绿色表示），但是，这个模型也存在误差，服从正态分布。

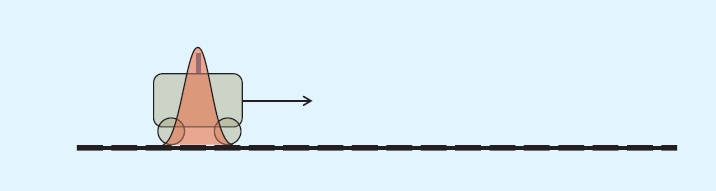
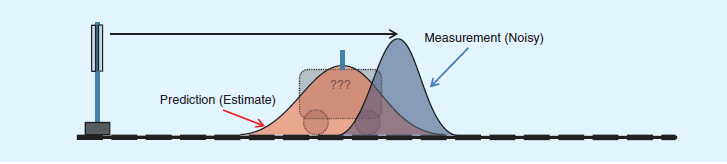
综上，kalman滤波可以看做是对预测模型和观测模型进行加权处理，获取更加接近实际值新的状态估计值。实际上，kalman滤波即是利用观测模型的残差来修正预测模型（最优估计），同时计算残差的权值。  

 递推方程

kalman滤波器用于估计离散时间过程的状态变量\(x\in\Re^{n}\)，这个离散时间过程由以下离散随机差分方程描述：

设\(\mathbf{x}_{k}^{-}\in\Re^{n}\)(-代表先验，^代表估计)为在已知第 k步以前状态情况下第 k 步的先验状态估计。\(\mathbf{\hat{x}}_{k}\in\Re^{n}\)为已知测量变量\(\mathbf{z}_{k}\)时第k步的后验状态估计。由此定义先验估计误差和后验估计误差： \[ \mathbf{e_{k}^{-}}=\mathbf{x_{k}} - \mathbf{\hat{x}_{k}^{-}}  ,  \mathbf{e_{k}}=\mathbf{x_{k}}  -  \mathbf{\hat{x}_{k}} \] 先验估计误差的协方差为： \[ \mathbf{P_{k}^{-}} = E[\mathbf{e_{k}^{-}}  \mathbf{(e_{k}^{-})^{T}}] \] 后验估计误差的协方差为： \[ \mathbf{P_{k}} = E[\mathbf{e_{k}}  \mathbf{(e_{k})^{T}}] \] 那么，对于预测和测量状态空间方程，即为：

预测空间模型-预测值（先验估计）： \[ \mathbf{\hat{x}_{k}^{-}}=\mathbf{A\hat{x}_{k-1}}+\mathbf{B{u}_{k-1}} \] 观测空间模型-测量值（测量值的预测）：
\[ \mathbf{\hat{z}_{k}}=\mathbf{H\hat{x}_{k}^{-}} \]

  实际测量值：$ = +  =  + $

这时，要在测量值的基础上再次更新状态变量\(x\)的先验估计，可得到后验估计，得到最优估计\(\mathbf{\hat{x}_{k}}\)： \[ \mathbf{\hat{x}_{k}} = \mathbf{\hat{x}_{k}^{-}} + \mathbf{K_{k}} (\mathbf{z_{k}} - \mathbf{H} \mathbf{\hat{x}_{k}^{-}}) \] 上式构造了kalman滤波器的表达式，先验估计\(\mathbf{\hat{x}_{k}^{-}}\)和加权的预测残差\((\mathbf{z_{k}} - \mathbf{H} \mathbf{\hat{x}_{k}^{-}})\)线性的构成了后验状态估计\(\mathbf{\hat{x}_{k}}\)。

递推方程的解释

（1） \(\mathbf{x_{k}}\) 的概率原型。这个可以见参考文献，来源于贝叶斯规则：\(\mathbf{\hat{x}_{k}}\)的更新取决于在已知先前的测量变量\(\mathbf{z_{k}}\)的情况下\(\mathbf{\hat{x}_{k}}\)的先验估计\(\mathbf{\hat{x}_{k}^{-}}\)的概率分布。在已知 \(\mathbf{z_{k}}\)的情况下，\(\mathbf{\hat{x}_{k}}\)的分布可写为： \[ p(\mathbf{x_{k}} | \mathbf{z_{k}}) - N(\mathbf{\hat{x}_{k}},\mathbf{P_{k}}) \] 即为正态分布。

（2） \(\mathbf{\hat{x}_{k}}\)的推导。关于\(\mathbf{\hat{x}_{k}}\)的形式，利用最优估计的原理，可以用极大似然估计可以推导，在论文中还看到过一种是将预测和测量的正态分布相乘求联合正态分布，联合正态分布即为后验状态估计。这里应该可以用反馈的原理来解释（如下面这张图），以测量值作为反馈，来进一步修正状态变量\(x\)的先验估计\(\mathbf{\hat{x}_{k}^{-}}\)，得到后验估计\(\mathbf{\hat{x}_{k}}\)。

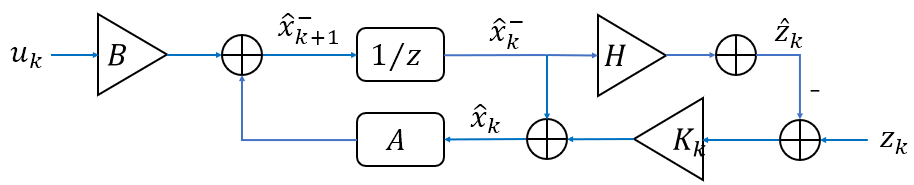
（3） \(\mathbf{K_{k}}\)的推导。既然\(\mathbf{\hat{x}_{k}}\)是\(\mathbf{x_{k}}\)的最优估计，那么\(\mathbf{x_{k}}\)的误差协方差矩阵的迹\(tr[\mathbf{P_{k}}]\)(\(\mathbf{P_{k}}\)的计算见下面)最小，即\(\mathbf{x_{k}}\)的均方误差最小。此时，将后验估计\(\mathbf{\hat{x}_{k}}\)的表达式和误差协方差矩阵\(\mathbf{P_{k}}\)的表达式联立，即可求得\(tr[\mathbf{P_{k}}]\)，对其求导，导函数为零时求得\(\mathbf{K_{k}}\)： \[ \mathbf{K_{k}} = \mathbf{P_{k}^{-}}\mathbf{H^{T}}(\mathbf{H}\mathbf{P_{k}^{-}}\mathbf{H^{T}}+\mathbf{R})^{-1}=  \frac{\mathbf{P_{k}^{-}}\mathbf{H^{T}}}{\mathbf{H}\mathbf{P_{k}^{-}}\mathbf{H^{T}}+\mathbf{R}} \]

 离散Kalman滤波算法

卡尔曼滤波器用反馈控制的方法估计过程状态：滤波器估计某一时刻的过程状态，然后以测量变量（含噪声）的方式获得反馈。

因此卡尔曼滤波器可分为两个部分：时间更新方程和测量更新方程。时间更新方程负责及时向前推算当前状态变量和误差协方差估计的值，以便为下一个时间状态构造先验估计。测量更新方程负责反馈，它将先验估计和新的测量变量结合以构造改进的后验估计。时间更新方程也可视为预估方程，测量更新方程可视为校正方程。最后的估计算法成为一种具有数值解的预估－校正算法。

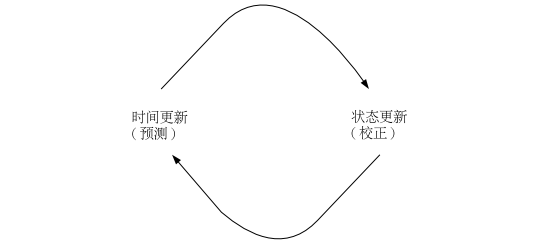
离散卡尔曼滤波时间更新方程 \[ \left\{\begin{matrix} \mathbf{\hat{x}_{k}^{-}}=\mathbf{A\hat{x}_{k-1}}+\mathbf{Bu_{k-1}} \\  \mathbf{P_{k}^{-}}=\mathbf{A} \boldsymbol{P_{k-1}} \mathbf{A^{T}} + \mathbf{Q} \end{matrix}\right. \] 时间更新方程主要获取由预测方程预测的k时刻的状态\(\mathbf{\hat{x}_{k}^{-}}\)，为\(\mathbf{\hat{x}_{k}}\)的先验状态估计；此时，其误差的协方差矩阵为\(\mathbf{P_{k}^{-}}\)。

  上式中，存在未知参数\(\mathbf{A}\), \(\mathbf{B}\), \(\mathbf{P_{k}^{-}}\), \(\mathbf{P_{k-1}}\), \(\mathbf{Q}\)  (1) 关于\(\mathbf{A}\)。这是和状态向量相关的矩阵，具体见举例  (2) 关于\(\mathbf{B}\)。这是驱动矩阵，和外部输入驱动有关，具体见举例  (3) 关于 \(\mathbf{P_{k}^{-}}\)。这是k时刻的先验状态估计的误差协方差矩阵，与预测方程的噪声有关，是根据（k-1）时刻的误差协方差矩阵\(\mathbf{P_{k-1}}\)递推而来（\(\mathbf{P_{k-1}}\)一般是给定的初值），利用\(\mathbf{P_{k}^{-}}\)的表达式 \(\mathbf{P_{k}^{-}} = E[\mathbf{e_{k}^{-}}  \mathbf{(e_{k}^{-})^{T}}]\)即可求得。  (4) 关于\(\mathbf{P_{k-1}}\)。（k-1）时刻的误差协方差矩阵（\(\mathbf{P_{k-1}}\)一般是给定的初值）  (5) 关于\(\mathbf{Q}\)。过程噪声（预测误差）\(\mathbf{w_{k-1}}\)的协方差矩阵，在预测的过程中产生。

离散卡尔曼滤波状态更新方程 \[ \left\{\begin{matrix} \mathbf{K_{k}} = \mathbf{P_{k}^{-}}\mathbf{H^{T}}(\mathbf{H}\mathbf{P_{k}^{-}}\mathbf{H^{T}}+\mathbf{R})^{-1} \\ \mathbf{\hat{x}_{k}} = \mathbf{\hat{x}_{k}^{-}} + \mathbf{K_{k}} (\mathbf{z_{k}} - \mathbf{H} \mathbf{\hat{x}_{k}^{-}}) \\  \mathbf{P_{k}}=(\mathbf{I} - \mathbf{K_{k}}\mathbf{H} )\mathbf{P_{k}^{-}} \end{matrix}\right. \] 状态更新方程在预测的先验估计\(\mathbf{\hat{x}_{k}^{-}}\)上，同测量值\(\mathbf{z_{k}}\)进行融合，更新校正先验状态估计，得到k时刻的后验状态估计\(\mathbf{\hat{x}_{k}}\)；此时，递推出后验状态估计的误差协方差矩阵\(\mathbf{P_{k}}\)，由此可以得到MMSE的条件，求得\(\mathbf{K_{k}}\)

  上式中，存在未知参数\(\mathbf{K_{k}}\), \(\mathbf{H}\), \(\mathbf{R}\), \(\mathbf{z_{k}}\), \(\mathbf{P_{k}}\)  (1) 关于\(\mathbf{K_{k}}\)。残差（真实测量值与基于先验状态估计的测量值（估计量））的增益，可以看做测量反馈的增益  (2) 关于\(\mathbf{H}\)。这是观测矩阵，和状态向量有关，具体见举例  (3) 关于\(\mathbf{R}\)。测量噪声（测量误差）\(\mathbf{v_{k-1}}\)的协方差矩阵，在测量的过程中产生。   (4) 关于\(\mathbf{z_{k}}\)。k时刻的真是测量值。  (5) 关于\(\mathbf{P_{k}}\)。k时刻的后验估计的误差协方差矩阵。

因此，通过时间更新和测量更新的不断递推，便可得到比较准确的状态向量估计值。其中，若初始过程噪声\(w_{k}\)和测量噪声\(v_{k}\)为一确定值，不断递推后状态向量误差协方差矩阵\(\mathbf{P_{k}}\)和卡尔曼增益\(\mathbf{K_{k}}\)会收敛并保持常量。下图显示了滤波器整个操作流程。

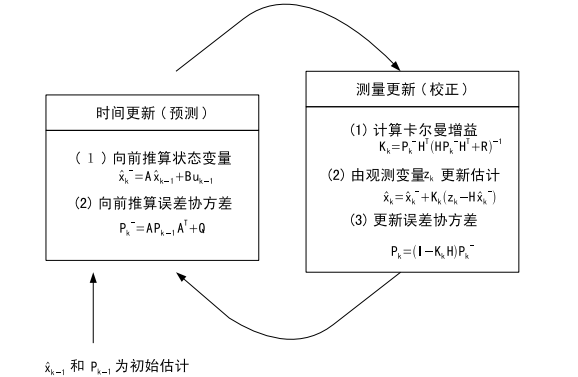
程序

 Matlab程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
% kalman filter

% x(k+1) = Fk * x(k) + Wk; 预测模型
% y(k)   = Hk * x(k) + Vk; 观测模型

N = 365;

Fk = [1];               % 状态转移矩阵               
X  = zeros(N,1);        % 初始化状态变量
W  = 12*randn(N,1);     % 构造过程噪声
X(1) = 100;             % 初始状态
                    
for k = 2:N
    % 状态方程
    X(k) = Fk * X(k-1) + W(k-1);
end

Hk = [2];               % 观测矩阵                
Y  = zeros(N,1);        % 初始化观测变量
V  = 20*randn(N,1);     % 构造观测噪声

for k = 1:N
    % 观测方程
    Y(k) = Hk * X(k) + V(k);   
end

Q  = cov(W);            % 过程噪声协方差；    
R  = cov(V);            % 观测噪声协方差；          

Xupdate = zeros(N,1);   
Xupdate(1) = Y(1);      % 初始化第一个，也就是观测到的第一个 
Pupdate(1) = 0;
for k = 2:N
    % 五大核心方程
    Xpredict(k) = Fk * Xupdate(k-1);
    Ppredict(k) = Fk * Pupdate(k-1) * Fk' + Q;
    K = Ppredict(k) * Hk * (Hk * Ppredict(k) * Hk' + R).^-1;
    Xupdate(k) = (1 - K * Hk) * Xpredict(k) + K * Y(k);
    Pupdate(k) = (1 - K * Hk) * Ppredict(k);
end

plot(1:N,X,'B','linewidth',2);hold on;
plot(1:N,Y,'K','linewidth',2);hold on;
plot(1:N,Xupdate,'R','linewidth',2);hold on;
plot(1:N,abs(Xupdate-X),'m','linewidth',2);hold off;
legend('真值','观测值','滤波值','误差')

参考

  • https://www.zhihu.com/question/23971601  
  • http://blog.csdn.net/xiahouzuoxin/article/details/39582483  
  • https://zhuanlan.zhihu.com/p/21889676  
  • https://zh.wikipedia.org/wiki/%E5%8D%A1%E5%B0%94%E6%9B%BC%E6%BB%A4%E6%B3%A2  
  • https://zh.wikipedia.org/wiki/%E6%9C%80%E5%B0%8F%E4%BA%8C%E4%B9%98%E6%B3%95
  • http://www.jianshu.com/p/2768642e3abf
  • http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/
  • Ramsey Faragher. Understanding the Basis of the Kalman Filter. 2012
  • Greg Welch, Gary Bishop. An Introduction to the Kalman Filter. 2001
  • Don Johnson. Minimum Mean Squared Error Estimators. 2004
  • R.E.Kalman. A new approach to linear filtering and prediction problems. 1960