张正友标定法是基于单平面棋盘格的相机标定方法，由张正友博士在1998年的论文："A Flexible New Technique for Camera Calibration"中提出，该方法介于传统的标定方法和自标定方法之间，使用简单实用性强，克服了传统标定法需要的高精度标定物的缺点，而仅需使用一个打印出来的棋盘格即可，便于操作，因此，广泛用于计算机视觉领域。

概述

相机的基本成像模型和标定是计算机视觉的基础，本文主要阐述单目相机成像的基本数学模型，并在此基础上对张正友标定法进行了讲解，最后通过C++代码实现。

相机模型

针孔相机模型

相机的成像过程基本是：现实世界-透镜中心-传感器成像-像素图像，应用小孔成像原理，可以建立现实世界的三维点和图片像素点之间的对应关系，即世界坐标系中的点和像素坐标系中的像素之间的几何关系。

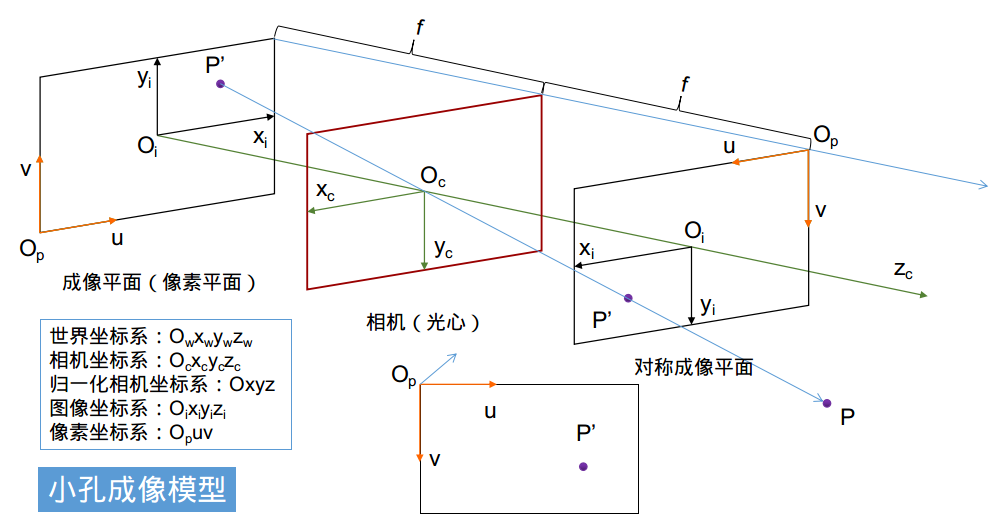
假定世界坐标系中一点$P_{w}(x_{w},y_{w},z_{w})$，通过相机光心$O_{c}$投射到相机传感器上，即相机的物理成像平面，该投射点在相机坐标系中的坐标为$P_{c}(x_{c},y_{c},z_{c})$，在像素坐标系下的坐标为$P'_{p}(u,v)$，这里，就是要建立$P_{w}(x_{w},y_{w},z_{w})$和$P'_{p}(u,v)$之间的变换关系。

坐标系

相机成像系统中，共包含四个坐标系：

世界坐标系$O(x_{w},y_{w},z_{w})$。世界坐标系固定不变，可作为绝对参考，一般主要关注相机坐标系和世界坐标系之间的旋转变换关系。单位是米。
相机坐标系$O(x_{c},y_{c},z_{c})$。在相机镜片上，以相机光心为原点，是相机成像模型中最重要的计算坐标系，相机在世界坐标系中的位姿通过相机坐标系相对世界坐标系的变换矩阵来表示。单位是米。
归一化相机坐标系$O(x,y,1)$。针对世界坐标系中任一点，在相机坐标系下归一化后得到与相机平面平行的面，它位于相机前方z=1处的平面上，称为归一化平面，此时，该坐标系上的点退化成二维点，通过某种映射关系（内参矩阵）可得到像素坐标。
图像坐标系$O(x_{i},y_{i})$。在相机传感器上，以物理成像平面和相机坐标系z轴延长线相交点为原点，将成像平面对称到相机前方，可得到图像是正着的对称成像平面，便于实际计算。x、y方向上和相机坐标系是相等的，单位是毫米。
像素坐标系$O(u,v)$。像素坐标系的原点在图像的左上角，即矩阵表示形式的起点。单位是像素。

在单目相机的成像模型中，坐标系间的变换关系如下：

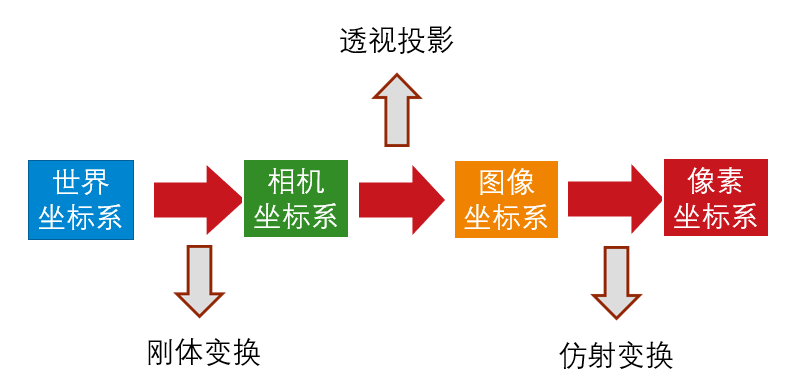
基本投影几何

像素坐标-图像坐标

像素坐标和图像坐标之间相差了一个缩放和原点的平移，假设在$u$轴上倍数为$1/dx$，在$v$轴上倍数为$1/dy$，同时，原点平移了[$c_{x}$,$c_{y}$]。假设传感器的横边和纵边之间的角度为90°(表示无误差），点$P'$像素坐标系下$P'_{p}(u,v)$和图像坐标系下$P'_{i}(x'_{i},y'_{i})$之间的关系为： \[ \begin{bmatrix}u\\ v\\ 1\end{bmatrix}= \begin{bmatrix}\frac{1}{\mathrm{d}x} x'_{i} + c_{x}\\ \frac{1}{\mathrm{d}y} y'_{i} + c_{y}\\ 1\end{bmatrix}= \begin{bmatrix}\frac{1}{\mathrm{d}x} & 0 & c_{x}\\ 0 & \frac{1}{\mathrm{d}y} & c_{y}\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix}x'_{i}\\ y'_{i} \\ 1\end{bmatrix} \] 其中，$1/dx$、$1/dx$单位为像素/毫米，表示一个像素在相机感光板上的物理长度；$c_{x}$、$c_{y}$单位为像素，表示相机感光板中心在像素坐标系下的坐标。

像素坐标-相机坐标

通过透视变换，相似三角形几何关系，在相机坐标系下，从点$P_{c}(x_{c},y_{c},z_{c})$到点$P'_{c}(x'_{c},y'_{c},z'_{c})$的投影模型表示为： \[ \frac{z_{c}}{z'_{c}}=\frac{z_{c}}{f}=-\frac{x_{c}}{x'_{c}}=-\frac{y_{c}}{y'_{c}} \] 将$P'_{c}$放到对称成像平面上（以后以此替代成像平面），则有： \[ \left\{\begin{matrix} x'_{c} = f \frac{x_{c}}{z_{c}} \\ y'_{c} = f \frac{y_{c}}{z_{c}} \end{matrix}\right. \] 将上式代入像素坐标的变换中，这里$x'_{c}=x'_{i}$、$y'_{c}=x'_{i}$，可以得到： \[ \left\{\begin{matrix} u = f_{x} \frac{x_{c}}{z_{c}} + c_{x} \\ v = f_{y} \frac{y_{c}}{z_{c}} + c_{y} \end{matrix}\right. \] 其中，$f_{x}=\frac{1}{\mathrm{d}x} f$、$f_{y}=\frac{1}{\mathrm{d}y} f$，$f_{x}$、$f_{y}$单位为像素。写成矩阵形式，有： \[ {z_{c}}{P'_{p}}= {z_{c}} \begin{bmatrix}u\\ v\\ 1\end{bmatrix} = \begin{bmatrix}\frac{1}{\mathrm{d}x} & 0 & c_{x}\\ 0 & \frac{1}{\mathrm{d}y} & c_{y}\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix}f & 0 & 0\\ 0 & f & 0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix}x_{c}\\ y_{c} \\ 1\end{bmatrix}= \begin{bmatrix}f_{x} & 0 & c_{x}\\ 0 & f_{y} & c_{y}\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix}x_{c}\\ y_{c} \\ z_{c}\end{bmatrix} = KP_{c} \] 其中，$K$为相机内参矩阵，相机的内参出厂后是不变的（不要拧动镜头，会影响焦距），可通过标定得到。至此，建立了像素点坐标$P'_{p}(u,v)$和P在相机坐标系中的点$P_{c}(x_{c},y_{c},z_{c})$之间的数学关系。

像素坐标-世界坐标

至此，需要建立相机坐标系下$P_{c}(x_{c},y_{c},z_{c})$和世界坐标系下$P_{w}(x_{w},y_{w},z_{w})$之间的数学关系，二者是同一点在不同坐标系下的表示，可通过变换矩阵来表示： \[ z_{c}P'_{p}= KP_{c}= K(RP_{w}+t) \] 其中，$R$为3×3旋转矩阵，$t$为3×1平移向量，为相机相对世界坐标系的位姿。

以上等式进行齐次化，将最后一维进行归一化处理，整理得到： \[ z_{c}P'_{p}= z_{c}\begin{bmatrix}u\\ v\\ 1\end{bmatrix} = \begin{bmatrix}f_{x} & 0 & c_{x}\\ 0 & f_{y} & c_{y}\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix}x_{c}\\ y_{c} \\ z_{c}\end{bmatrix} = \begin{bmatrix}f_{x} & 0 & c_{x} & 0\\ 0 & f_{y} & c_{y} & 0\\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix}R & t \\ \vec{0} & 1\end{bmatrix} \begin{bmatrix}x_{w}\\ y_{w} \\ z_{w} \\ 1\end{bmatrix} = KTP_{w} \] 其中，$T$为相机外参，即相机坐标系相对世界坐标系的变换矩阵，相机位姿改变，则外参T会随之变化。关于外参，这个主要涉及坐标变换的知识，因为对这一块比较熟悉，因此具体内容略去。至此，在不考虑畸变的情况下，建立了像素坐标系下点$P'_{p}(u,v)$和世界坐标系下点之间$P_{w}(x_{w},y_{w},z_{w})$的几何关系。

归一化相机平面

在像素坐标-相机坐标的模型中，按照齐次坐标的方式，可以将$z_{c}$约去，$P_{c}(x_{c},y_{c},z_{c})$变为$P_{c}(\frac{x_{c}}{z_{c}},\frac{y_{c}}{z_{c}},1)$，此时得到$P$在相机归一化平面上的投影，有如下关系： \[ {P'_{p}}= \begin{bmatrix}u\\ v\\ 1\end{bmatrix} = \begin{bmatrix}f_{x} & 0 & c_{x}\\ 0 & f_{y} & c_{y}\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix}\frac{x_{c}}{z_{c}}\\ \frac{y_{c}}{z_{c}} \\ 1\end{bmatrix} = K \begin{bmatrix}x\\ y \\ 1\end{bmatrix} = KP_{c} \] 这时，可以将$P_{c}(\frac{x_{c}}{z_{c}},\frac{y_{c}}{z_{c}},1)$看做一个二维点，这里记为$P_{c}(x,y,1)$，它位于相机前方z=1处的平面上，该平面称为相机归一化平面。

透镜畸变

畸变包括径向畸变和切向畸变，其中，径向畸变主要由透镜形状引起，有桶形畸变和枕形畸变，由于透镜的加工往往时中心对称的，不规则的畸变通常是径向对称。切向畸变是相机在组装时不能是透镜和成像面严格平行造成的。

对于径向畸变，可以用与距中心距离有关的二次及高次多项式函数进行纠正，在相机归一化坐标系中，有： \[ \left\{\begin{matrix} x_{d} = x(1 + k_{1}r^2 + k_{2}r^4 + k_{3}r^6) \\ y_{d} = y (1 + k_{1}r^2 + k_{2}r^4 + k_{3}r^6) \end{matrix}\right. \] 其中，$\begin{bmatrix}x, y\end{bmatrix}^T$是归一化相机平面的坐标，$\begin{bmatrix}x_{d}, y_{d}\end{bmatrix}^T$是归一化相机平面引入畸变的坐标，$r^2 = x^2+y^2$。

对于切向畸变，其纠正方式如下： \[ \left\{\begin{matrix} x_{d} = x + 2p_{1}xy + p_{2}(r^2 + 2x^2) \\ y_{d} = y + p_{1}(r^2 + 2y^2) + 2p_{2}xy \end{matrix}\right. \] 结合径向畸变和切向畸变，可以求出归一化相机坐标系下原始图像的实际坐标： \[ \left\{\begin{matrix} x_{d} = x(1 + k_{1}r^2 + k_{2}r^4 + k_{3}r^6) + 2p_{1}xy + p_{2}(r^2 + 2x^2) \\ y_{d} = y (1 + k_{1}r^2 + k_{2}r^4 + k_{3}r^6) + p_{1}(r^2 + 2y^2) + 2p_{2}xy \end{matrix}\right. \] 两种畸变最后都归结到五个参数：$k_{1}$、$k_{2}$、$p_{1}$、$p_{2}$、$k_{3}$，注意，此为OpenCV畸变系数的书写顺序。通过内参矩阵将归一化相机坐标转换到像素平面，得到该点在图像上的正确位置（此时图像是带畸变的）： \[ \left\{\begin{matrix} u_{d} = f_{x} x_{d} + c_{x} \\ v_{d} = f_{y} y_{d} + c_{y} \end{matrix}\right. \] 这里，如果拿到了带畸变的图像再去畸变，则是要通过带畸变的$\begin{bmatrix}u_{d}, v_{d}\end{bmatrix}^T$得到去畸变的$\begin{bmatrix}u, v\end{bmatrix}^T$，这是以上推导的逆过程，即是通过$\begin{bmatrix}u_{d}, v_{d}\end{bmatrix}^T$反求$\begin{bmatrix}x_{d}, y_{d}\end{bmatrix}^T$，然后通过迭代的方式求解$\begin{bmatrix}x, y\end{bmatrix}^T$，可参考OpenCV去畸变迭代解法，最后通过内参矩阵将归一化相机坐标转换到像素平面，得到去畸变的$\begin{bmatrix}u, v\end{bmatrix}^T$，有： \[ \left\{\begin{matrix} u = f_{x} x + c_{x} \\ v = f_{y} y + c_{y} \end{matrix}\right. \]

相机标定

相机标定的目的有2个：

第一个目的就是获得相机的内参矩阵$K$和外参矩阵$T$，其中，$K$是固定不变的，$T$会随着相机位姿变换而改变。
第二个目的就是获得相机的畸变系数：$k_{1}$、$k_{2}$、$p_{1}$、$p_{2}$、$k_{3}$。

在张正友标定中，从不同角度拍15-20张棋盘格照片，就可以求解相机的内参、外参和畸变系数。

棋盘格标定板

平面的单应性被定义为从一个平面到另一个平面的投影映射，下图中的二维平面上的棋盘格角点映射到相机成像仪上的映射就是平面单应性的例子。假定世界坐标系原点在标定板第一个角点，此时，物理世界的点$P_{w}(x_{w},y_{w},0)$通过投影映射到像素坐标$P'_{p}(u,v)$。

已知条件：已知棋盘格实际大小尺寸，如12×9格、每格30mm，就知道物理世界中角点的世界坐标；通过相机成像拿到图像，再通过角点检测算法检测角点，就知道与物理世界对应的角点的像素坐标。

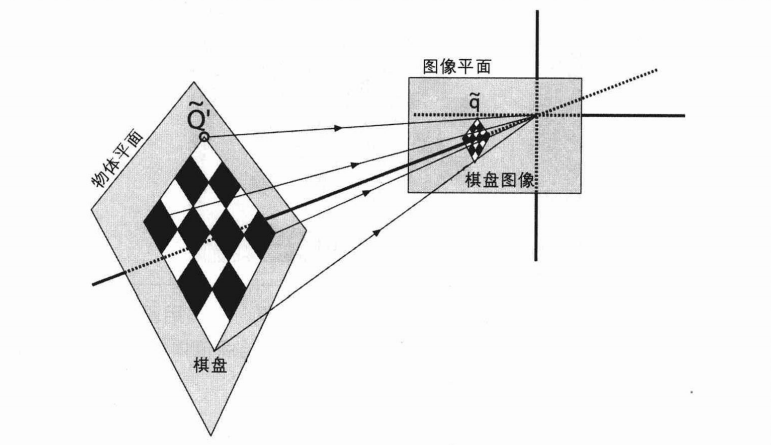
单应性矩阵

由上述推导可知，不考虑畸变，对于世界坐标系单点$P_{w}(x_{w},y_{w},z_{w})$投影到像素坐标系中$P'_{p}(u,v)$，令$z_{w}=0$，稍作调整，其数学模型如下： \[ s P’_{p}= s\begin{bmatrix}u\\ v\\ 1\end{bmatrix} = \begin{bmatrix}f_{x} & \gamma & c_{x}\\ 0 & f_{y} & c_{y}\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix}r_{1} & r_{2} & r_{3} & t \end{bmatrix} \begin{bmatrix}x_{w}\\ y_{w} \\ 0 \\ 1\end{bmatrix} = K\begin{bmatrix}r_{1} & r_{2} & t \end{bmatrix} \begin{bmatrix}x_{w}\\ y_{w} \\ 1\end{bmatrix} = KTP_{w} \] 其中，$s$为尺度因子，$\gamma$为考虑传感器的横边和纵边之间的角度误差（角度为90°表示无误差，此时$\gamma$=0），上式中可忽略$r_{3}$。令$H=K\begin{bmatrix}r_{1} & r_{2} & t \end{bmatrix}$，则有 \[ s P’_{p}= s\begin{bmatrix}u\\ v\\ 1\end{bmatrix} = \begin{bmatrix}H_{11} & H_{12} & H_{13}\\ H_{21} & H_{22} & H_{23}\\ H_{31} & H_{32} & H_{33} \end{bmatrix} \begin{bmatrix}x_{w}\\ y_{w} \\ 1\end{bmatrix} = HP_{w} \] 上式中，单点$P_{w}$和$P'_{p}$是已知的，则根据已知点坐标求解$H$，$H$称为单应性矩阵。展开方程消去尺度因子$s$、$\lambda$，得到 \[ \left\{\begin{matrix} H_{33}u = H_{11} x_{w} + H_{12} y_{w} + H_{13} - H_{31} x_{w}u - H_{32} y_{w}u \\ H_{33}v = H_{11} x_{w} + H_{12} y_{w} + H_{13} - H_{31} x_{w}v - H_{32} y_{w}v \end{matrix}\right. \] 上式中，一个点对提供两个约束方程。$H$为齐次矩阵，可成倍放大或缩小，共8个独立元素，令$H_{33}=1$或者令矩阵模变为1，通过单张棋盘格照片中的4个角点可以提供8个约束方程，通过线性方程求解的方法称为直接线性变换法。当一张图片上的标定板角点数量大于4时，利用最小二乘法回归最佳的矩阵 $H$，每张照片对应一个$H$。至此，完成$H$的求解（注意：这里求得的$H$最后一个元素进行了归一化，实际的$H$是带尺度因子的，后面涉及到$H$的表示时不加尺度因子，但是计算需要加上尺度因子）。

内参的求解

在求得单应性矩阵$H$的基础上，进一步求取内参。可知旋转矩阵$R$为单位正交矩阵，满足以下关系： \[ \left\{\begin{matrix} r_{1}^Tr_{2}=0 \\ r_{1}^Tr_{1} = r_{2}^Tr_{2} = 1 \end{matrix}\right. \] 同时，根据$H$的定义，令$H=\begin{bmatrix}H_{1} & H_{2} & H_{3} \end{bmatrix}=K\begin{bmatrix}r_{1} & r_{2} & t \end{bmatrix}$，可以得到： \[ \left\{\begin{matrix} r_{1}=K^{-1}H_{1} \\ r_{2}=K^{-1}H_{2} \end{matrix}\right. \] 结合以上二式，通过$r_{1}$、$ r_{2}$单位正交得到的约束方程，则有： \[ \left\{\begin{matrix} H_{1}^T B H_{2} = 0 \\ H_{1}^T B H_{1} = H_{2}^T B H_{2} = 1 \end{matrix}\right. \] 其中，$B=K^{-T} K^{-1}$，B为对称矩阵，共6个元素。按照内参矩阵展开得到$B$： \[ B = K^{-T} K^{-1} = \begin{bmatrix}\frac{1}{f_{x}^2} & -\frac{\gamma}{f_{x}^2f_{y}} & \frac{\gamma c_{y}-f_{y}c_{x}}{f_{x}^2f_{y}} \\ -\frac{\gamma}{f_{x}^2f_{y}} & \frac{1}{f_{y}^2} + \frac{\gamma^2}{f_{x}^2f_{y}^2} & \frac{\gamma (f_{y}c_{x}-\gamma c_{y})}{f_{x}^2f_{y}^2}-\frac{c_{y}}{f_{y}^2} \\ \frac{\gamma c_{y} -f_{y}c_{x}}{f_{x}^2f_{y}} & \frac{\gamma(f_{y}c_{x} -\gamma c_{y})}{f_{x}^2f_{y}^2}-\frac{c_{y}}{f_{y}^2} & \frac{(f_{y}c_{x}-\gamma c_{y})^2}{f_{x}^2f_{y}^2}+\frac{c_{y}^2}{f_{y}^2}+1 \end{bmatrix} = \begin{bmatrix}B_{11} & B_{12} & B_{13} \\ B_{12} & B_{22}& B_{23} \\ B_{13} & B_{23} & B_{33} \end{bmatrix} \] 为了求解矩阵$B$，需要计算$H_{i}^TBH_{j}^T$ ： \[ H_{i}^TBH_{j}^T= \begin{bmatrix}H_{1i} & H_{2i} & H_{3i} \end{bmatrix} \begin{bmatrix}B_{11} & B_{12} & B_{13} \\ B_{12} & B_{22}& B_{23} \\ B_{13} & B_{23} & B_{33} \end{bmatrix} \begin{bmatrix}H_{1i} \\ H_{2i} \\ H_{3i} \end{bmatrix}= v_{ij}b \]

其中，$v_{ij}$、$b$分别记为： \[ v_{ij} = \begin{bmatrix}H_{1i}H_{1j} & H_{1i}H_{2j}+H_{2i}H_{1j} & H_{2i}H_{2j} & H_{1i}H_{3j}+H_{3i}H_{1j} & H_{2i}H_{3j}+H_{3i}H_{2j} & H_{3i}H_{3j}\end{bmatrix}^T \]

\[ b = \begin{bmatrix}B_{11} & B_{12} & B_{22} & B_{13} & B_{23} & B_{33}\end{bmatrix}^T \]

此时，通过$r_{1}$、$ r_{2}$单位正交得到的约束方程可化为： \[ \begin{bmatrix}v_{12}^T \\ v_{11}^T -v_{22}^T \end{bmatrix} b =vb =0 \] 矩阵$v$全部由单应性矩阵$H$的元素构成，因此矩阵$v$已知，每个$H$对应一个$v$，因为内参不变，所以处在每个位姿的相机可以提供一个$v$。$b$中有6个独立元素，每个$v$可构成两个约束方程，所以最少需要3张不同位姿的照片才能求解向量$b$。当棋盘格图片的个数大于3时（事实上一般需要15到20张标定板图片），可采用最小二乘拟合最佳的向量 $b$，并得到矩阵 $B$，可以计算内参矩阵$K$中每个元素。

考虑单应性矩阵$H$带有尺度因子，$B$由$H$中的元素构成，这里引入尺度因子$\lambda$进行矫正： \[ B=\lambda K^{-T} K^{-1} \] 通过最终解算，可以得到： \[ \begin{matrix} c_{y} = (B_{12}B_{13}-B_{11}B_{23})/(B_{11}B_{22}-B_{12}^2) \\ \lambda = B_{33} - [B_{13}^2+c_{y}(B_{12}B_{13}-B_{11}B_{23})]/{B_{11}} \\ f_{x} = \sqrt{\lambda/B_{11}} \\ f_{y} = \sqrt{\lambda B_{11}/(B_{11}B_{22}-B_{12}^2)} \\ \gamma = -B_{12}f_{x}^2f_{y}/\lambda \\ c_{x} = \gamma c_{y}/f_{x} - B_{13}f_{x}^2/\lambda \end{matrix} \] 至此，完成内参矩阵$K$的求解。

外参的求解

在求得单应性矩阵$H$和内参矩阵$K$的基础上，结合$H=K\begin{bmatrix}r_{1} & r_{2} & t \end{bmatrix}$和$T=\begin{bmatrix}r_{1} & r_{2} & r_{3} & t \end{bmatrix}$，$r_{1}$、$r_{2}$、$t$可以求解，考虑单应性矩阵$H$带有尺度因子，引入尺度因子$\hat{\lambda}$进行矫正： \[ \left\{\begin{matrix} r_{1} = \hat{\lambda} K^{-1} H_{1} \\ r_{2} = \hat{\lambda} K^{-1} H_{2} \\ t = \hat{\lambda} K^{-1} H_{3} \end{matrix}\right. \] 根据上式可以求得这里的尺度因子$\hat{\lambda}$： \[ \hat{\lambda} = \frac{1}{||K^{-1}H_{1}||} = \frac{1}{||K^{-1}H_{2}||} \] 利用旋转矩阵的向量单位正交的特性，得到$r_{3}$： \[ r_{3} = r_{1}\times r_{2} \] 至此，完成外参矩阵$T$的求解。

畸变系数的求解

在不考虑畸变的情况下，以上求解可得到相机的内、外参，但是，实际中透镜引入的畸变会导致实际成像失真，而我们拍出来不做处理的图片是带有畸变的。假设理论无畸变像素$\begin{bmatrix}u, v\end{bmatrix}^T$，实际的像素坐标$\begin{bmatrix}u_{d}, v_{d}\end{bmatrix}^T$，理论无畸变归一化点坐标$\begin{bmatrix}x, y\end{bmatrix}^T$，实际的归一化点坐标$\begin{bmatrix}x_{d}, y_{d}\end{bmatrix}^T$，则有：

\[ \begin{matrix} \left\{\begin{matrix}u = f_{x} x + c_{x}\\ v = f_{y} y + c_{y}\end{matrix}\right. & \left\{\begin{matrix}u_{d} = f_{x} x_{d} + c_{x}\\ v_{d} = f_{y} y_{d} + c_{y}\end{matrix}\right. \end{matrix} \] 在张正友标定中，只考虑了影响畸变较大的径向畸变系数$k_{1}$、$k_{2}$，如下： \[ \left\{\begin{matrix} x_{d} = x(1 + k_{1}r^2 + k_{2}r^4) \\ y_{d} = y (1 + k_{1}r^2 + k_{2}r^4) \end{matrix}\right. \] 结合以上二式，可以得到 \[ \begin{bmatrix}(u-c_{x})(x^{2}+y^{2}) & (u-c_{x})(x^{2}+y^{2})^{2} \\ (v-c_{y})(x^{2}+y^{2}) & (v-c_{y})(x^{2}+y^{2})^{2} \end{bmatrix} \begin{bmatrix} k_{1} \\ k_{2}\end{bmatrix} = \begin{bmatrix} u_{d}-c_{x} \\ u_{d}-c_{x}\end{bmatrix} \] 对于每一个角点，只要知道畸变后的像素坐标$\begin{bmatrix}u_{d}, v_{d}\end{bmatrix}^T$、理想的无畸变的像素坐标$\begin{bmatrix}u, v\end{bmatrix}^T$，$\begin{bmatrix}x, y\end{bmatrix}^T$也可以经过内参解算出来，就可以构造两个上述约束方程，需要求解未知数$k_{1}$、$k_{2}$。那么，有n幅图像，每幅图像上有m个标定板角点，可以得到2mn个约束方程，将约束方程系数矩阵记为$D$，等式右端非齐次项记为$d$，可将其记着矩阵形式： \[ Dk=d \] 这里可以用最小二乘法求解，最小二乘法的目标：求误差的最小平方和，根据代价函数的对应有两种：线性和非线性（取决于对应的残差(residual)是线性的还是非线性的）。非线性最小二乘没有封闭解，通常用迭代法求解；线性最小二乘的解是封闭解，如果x使$||Dx-d||$最小化，则x满足正规系方程$D^{T}Dx = D^{T}d$，$k$的线性最小二乘解可由下式给出： \[ k= \begin{bmatrix} k_{1} \\ k_{2} \end{bmatrix} = (D^{T}D)^{−1} D^{T}d \] 其中，内参、外参已知，$\begin{bmatrix}u_{d}, v_{d}\end{bmatrix}^T$可以从拍到的原始照片中获取，$\begin{bmatrix}u, v\end{bmatrix}^T$可以通过反投影近似求得，如下所示： \[ s\begin{bmatrix}u\\ v\\ 1\end{bmatrix} = K\begin{bmatrix}r_{1} & r_{2} & t \end{bmatrix} \begin{bmatrix}x_{w}\\ y_{w} \\ 1\end{bmatrix} = H \begin{bmatrix}x_{w}\\ y_{w} \\ 1\end{bmatrix} \] 在上式的基础上，消去尺度因子$s$，此处将$H$中的尺度因子也算到$s$中，可得： \[ \left\{\begin{matrix} u = \frac{H_{11} x_{w} + H_{12} y_{w} + H_{13}}{H_{31} x_{w} + H_{32} y_{w} + H_{33}} \\ v = \frac{H_{21} x_{w} + H_{22} y_{w} + H_{23}}{H_{31} x_{w} + H_{32} y_{w} + H_{33}} \end{matrix}\right. \] 至此，便可以求出畸变系数$k_{1}$、$k_{2}$。

这里有一个疑问，我的理解是这样的。实际拿到的照片是带有畸变的，但是在计算内、外参是使用的是无畸变像素像素坐标，这时，求得的内、外参是不是准确的。同时，求解畸变系数时需要提供带畸变和无畸变的像素坐标，而无畸变的像素坐标是使用在上一过程中的内、外参矩阵间接反投影得到的。反求的无畸变像素坐标和上一过程使用的不一样，因为内、外参矩阵是综合很多角点优化得到的。因此，再通过迭代求解对参数进行优化。

极大似然估计

通过理想无畸变像素求出初始内、外参后，根据内外、参可以得到物理世界点重新投影在成像平面后的像素坐标$\hat{P'}$。假设我们有棋盘格模型的n个图像，模型平面上有m个点，且图像上的噪声服从独立同一分布，令第i副图像上的角点$(P_{w})_{j}$在重投影得到的点$\hat{P'}$： \[ \hat{P'}(K,R_{i},t_{i},(P_{w})_{j})=K[R,t] (P_{w})_{j} \] 其中，$K$——相机内参，$R_{i}$——第i张图像的旋转矩阵，$t_{i}$——第i张图像的平移向量，$(P_{w})_{j}$——第j个角点对应的世界坐标。则角点$P'_{ij}$的概率密度函数为： \[ f(P'_{ij})=\frac{1}{\sqrt{2\pi}}e^{-\frac{(P'_{ij}-\hat{P'}(K,R_{i},t_{i},(P_{w})_{j})^2}{\sigma^2}} \] 构造最大似然估计： \[ L(P'_{ij}-\hat{P'}(K,R_{i},t_{i},(P_{w})_{j})= \prod_{i=1,j=1}^{n,m}f(P'_{ij})= \frac{1}{\sqrt{2\pi}}e^{-\frac{\sum_{i=1}^{n}\sum_{j=1}^{m}(P'_{ij}-\hat{P'}(K,R_{i},t_{i},(P_{w})_{j})^2}{\sigma^2}} \]

使用最小化负对数的方式来求高斯分布的最大似然，则最大似然估计可以通过最小化以下函数得到： \[ \sum_{i=1}^{n}\sum_{j=1}^{m}= \left \| P'_{ij}-\hat{P'}(K,R_{i},t_{i},(P_{w})_{j}) \right \|^2 \] 上式中，$P'_{ij}$——通过角点检测算法得到的第i张图像的第j个角点像素坐标。

那么，怎么令上面这个目标函数达到最小值呢？可以看出，这是一个非线性最小二乘问题，目的是通过估计参数$(K,R_{i},t_{i},P_{wj})$使重投影误差最小，可以通过列文伯格-马夸尔特方法（L-M方法）求解参数。关于L-M算法的具体内容，可在Matlab中进行验证，也可以利用ceres库和g2o库等工具构建，这里先不作叙述。

考虑畸变的影响时，新引入了两个参数$k_{1}$、$k_{2}$，则极大似然估计可以通过最小化以下函数得到： \[ \sum_{i=1}^{n}\sum_{j=1}^{m}= \left \| P'_{ij}-\hat{P'}(K,k_{1},k_{2},R_{i},t_{i},(P_{w})_{j}) \right \|^2 \] 因此，整个过程两次使用极大似然估计优化参数，第一次用来优化内、外参，使用优化的内、外参求解畸变系数，最后再一起优化内、外参和畸变系数。

相机标定的步骤

总结以上过程，标定的简要步骤如下：

准备一个张正友标定法的棋盘格，棋盘格大小已知，用相机对其进行不同角度的拍摄，得到一组15-20张图像；
对图像中的特征点如标定板角点进行检测，得到标定板角点的像素坐标值，根据已知的棋盘格大小和世界坐标系原点，计算得到标定板角点的物理坐标值；
求解内参矩阵与外参矩阵。根据物理坐标值和像素坐标值的关系，求出单应性矩阵$H$，进而构造$v$矩阵，求解$B$矩阵，利用$B$矩阵求解相机内参矩阵 $K$，最后求解每张图片对应的相机外参矩阵 $T$（旋转矩阵$R$和平移向量$t$），通过极大似然估计优化内、外参；
求解畸变参数。利用构造$D$矩阵，计算径向畸变参数；
综合内外参、畸变系数，利用极大似然估计对这些参数进行优化。

代码

基于张正友标定相机内参，详见C++实现代码zhangCalibration)

参考

A Flexible New Technique for Camera Calibration, zhang
https://zhuanlan.zhihu.com/p/94244568
学习Opencv，Gary Bradski & Adrian Kaebler
视觉SLAM十四讲，高翔
https://www.cnblogs.com/mtcnn/p/9411941.html

思无邪

相机模型与标定

概述